空気の温度を上げると膨張し、冷やすと収縮します。学校では、小学校の4年生で学びます。
この温度と体積の間には、何か美しい関係があるのではないか?
幾人かの科学者が研究し、18世紀、フランスのシャルルが結論を出します。
「空気は、0℃の体積を基準に、1℃上がることに273分の1ずつ体積が増えていく」
この規則性を使った計算問題が、中学入試でもしばしば取り上げられます。
規則性が、「0℃を基準にした時だけ成り立つ」ことを読み飛ばし、めちゃくちゃな計算になってお手上げの子が続出します。
今回、典型問題を、「温度と体積(膨張・収縮)」の「よくある問題」にまとめておきました。
また、この法則で出てくる273という数字は、絶対温度でも出てきます。
0℃を基準に、1℃で273分の1ずつ体積が変わるなら、1℃下がれば273分の1体積は減ります。100℃下がれば273分の100減り、ついに273℃下がれば、体積が0になります。
これは何を意味するか?
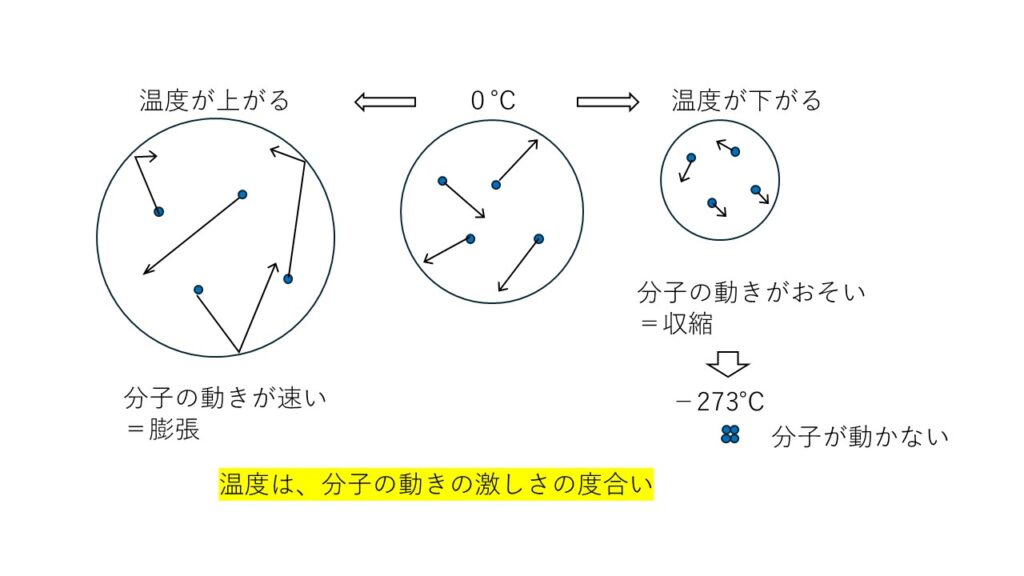
温度とは、分子の動きの激しさを言います。0℃の空気でも分子は激しく動き(音速の1.5倍の速さ)、温度を上げるとさらに激しく動きます。これが空気の体積の膨張になります。
温度を下げれば、分子の動きは弱くなって収縮し、ついに273℃下げれば、空気の体積は無くなり、分子は動かなくなるのです。
温度が分子の動きの激しさならば、これ以上温度を下げることはできません。
したがって、考えられる最低温度が-273℃となり、これを絶対0℃とよびます。
ただ、現実の世界にこの温度は無く、最も温度が低い宇宙空間でも、-270℃(絶対3℃)です。

